Linear Regression Solver

Download the Notebook

We are going to write a function to solve a linear regression. First Linear regression concepts are introduced.

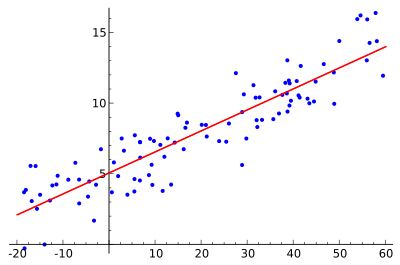
Linear Regression

Assume we want to find the best fit for the equation:

$$ Y = \beta _0 + \beta _1 X + e $$

What are the values for $\beta _0$ and $\beta _1$?

We need to optimize this function by minimization of errors which is:

$$ e = Y - \beta _0 - \beta _1 X $$

There could be more than one variable to fit:

$$ e = Y - \beta _0 - \beta _1 X_1 - \beta _2 X_2 - \beta _3 X_3 ... $$

We can write it in matrix notation like:

$$ e = Y - X\beta $$

The matrix $X$ contains all variables and $\beta$ contains all parameters. It is a bit easier way to write like this. We use the least square minimization for regression fits:

$$ \begin{align} \min{\beta} \quad e'e &= (Y−X\beta)′(Y−X\beta)\\ \, &= Y′Y−2\beta′X′Y+\beta′X′X\beta \end{align} $$

The solution is the partial derivative of sum of squares residuals with respect to $\beta$: $$ \frac{\partial e'e}{\beta} = −2X′Y+2X′X\beta = 0 \\ $$

So the $\beta$ is:

$$ \beta = (X′X)^{-1}X′Y $$

Well... It might seem confusing if you meet Least Squares first time but you will use it in Econometrics a lot. It is very basic concept but we are only interested in the solution/formula of the $\beta$ for now. We can define a function that fits the regression.

In [1]:
import numpy as np
In [2]:
def ols(x,y):
    # you need to make calculations inside the function and return the BETA coefficients
    return None # return Beta coefficients

Hints

  • First multiply $X'$ with X, then $X'$ with $Y$. Lastly multiply the two results.
  • For multiplication you should use the np.dot() function.
  • $X'$ means X.T in numpy format. For instance multiplication of $X'Y$ = np.dot(X.T,Y).
  • Use the numpy.linalg.inv() function to take the inverse of $(X'X)^{-1}$

Test

Test if your function works. For we need to create random values.

In [3]:
np.random.seed(1)
X = np.concatenate((np.ones((10,1)),np.random.random((10,3))), axis=1) 
Y = np.random.randint(10, size=(10,1))
In [4]:
print(ols(X,Y))

None